《TENET天能》中國大陸譯《信條》
觀賞”天能”時大家可能需要知道的最重要的物理解釋”熵”。
“熵”到底是什麼呢?
一般來說大家紹的方式是,一個孤立的系統中物質會從有序往無序的狀態發展。
也就是說”熵”只會增加不會減少,往最混亂的方向演化,因此從這個角度看,熵的測量也可以被看作是一種時間的指標,因為它永遠朝向一個目標。
上面這句話打個比方說就是,一個整齊的房間是低”熵”,一個亂七八糟的房間是高”熵”,在沒有外力介入的情況下,房間一定會從整齊的房間(低”熵”)往亂七八糟的房間(高”熵”)演化。(以後可以跟爸媽解釋房間亂的原因了o(^▽^)o)。
或是我們拿到一個新的樸克牌,牌的排列是從小到大按順序的(低”熵”),我們洗牌的次數越多,這副牌就會變得越來越無序(高”熵”),在這個系統中”熵”就是在慢慢的變大。
你在沙灘中堆起的一座沙堡(低”熵”),風很快就會讓沙堡消失(高”熵”),重新回歸無序,在厲害的風也永遠不可能把沙子吹成一座規則的沙堡形態。
聽完這三個比喻,或許你會感覺自己理解了什麼是熵,但我想說的是用無序和有序來理解熵,依然還是一種比喻,這樣的理解依然是模糊的,在遇到一些其他的例子的時候還是很容易產生誤解的。

例如,我們假設有2個盒子,每個盒子都有4塊積木塊,其中一個盒子的積木塊大致均勻的分佈在盒子中,而另一個盒子中的積木塊則是一邊多一邊少,現在我問你,這兩個盒子的熵值哪個更大呢?(如上圖所示)


這時候,如果再用有序或無序去考慮問題的話,可能就會有點犯糊塗了。 到底是盒子1更有序呢?還是盒子2更有序呢?
或許大多數人會認為盒子1更加有序,因為看起來更加整齊,但是答案卻恰恰相反。

從熵的角度看過去,盒子1的熵值更大,也就是更加無序,而盒子2的熵值更熵,更加有序,這是為什麼呢?

今天要教給你理解熵值更加準確得方法,就是考慮哪種狀態的可能性(機率)更高,

我們來分析一下,假如我們把這個盒子中的空間假想成一分為二,給積木編號1、2、3、4。
盒子1我們可以認為是四塊積木剛好一般各2塊,而盒子2則是左邊有1塊右邊有3塊積木。
先在請你思考一下,盒子1的這種分布方式的可能性總共有多少種呢?
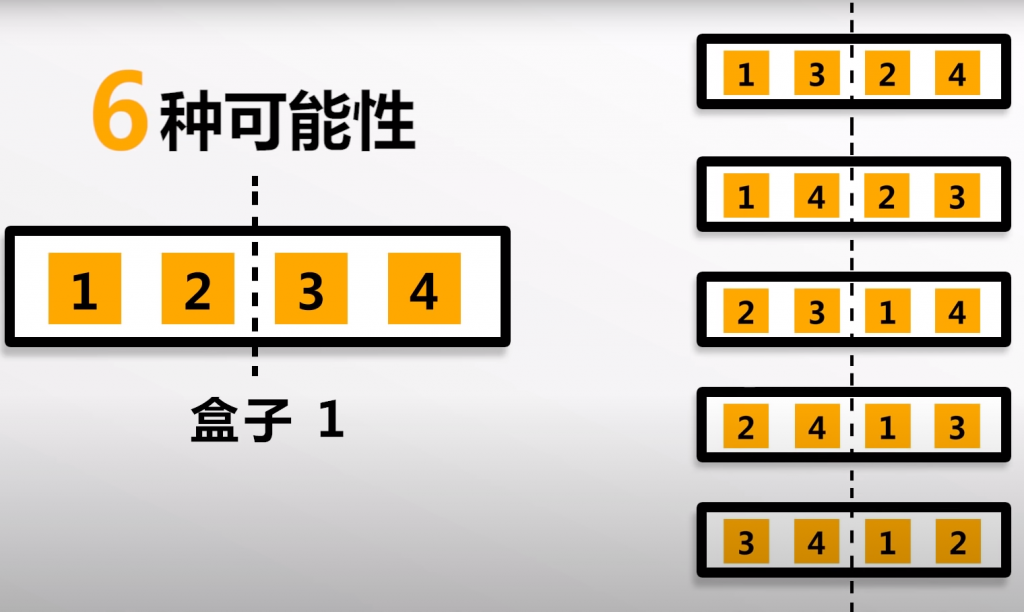
答案是6種可能性,相當於從4塊積木中任意選出2塊放到左邊的空間。
那盒子2的分布方式有多少種呢可能信呢?
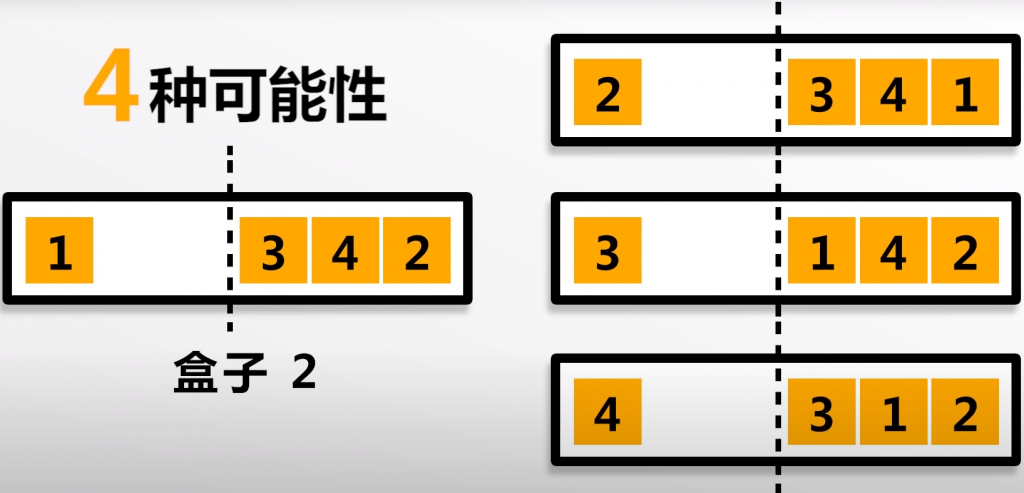
答案是4種可能性,相當於從4塊積木中任意取出1塊放到左邊的空間。
如果你理解了,那麼請你記住,熵值不斷增大的真正含意,是自然界會自發的朝者分布可能性(機率)更高的方向發展。
也就是說可能性(機率)越高”熵”值就越高,反之可能性(機率)越低”熵”值就越低。
如果你還沒想明白,我們來做個思想實驗,假設現在這是一個密封的長條狀盒子,盒子有一定的深度,這樣積木塊就可以自由地在裡面運動,不會堵塞。
我們把盒子拿起來,用力的搖一搖,然後把盒子放平穩,你覺得是出現盒子1的情況可能信更大呢?
還是出現盒子2的情況可能性更大呢?我想這次應該不難理解了吧!
顯然積木塊大致平均分布在盒子中的可能性是更大的,或許有些人還是在想,為什麼熵值會必然增加呢?在這個思想實驗中完全有可能也搖出盒子2的清況。
的確在這個例子中因為盒子1的可能性比盒子2的可能性大的不是很多,只要我們搖的次數足夠多,總還是會觀察到盒子2的情況的。
但是如果我們把積木塊的數量增加到1000個,那麼盒子1的可能性就要比盒子2,也就是999個積木都集中在右邊的可能性大到一個不可思議的程度,大約是10的300次方。
打個比方假如你從宇宙誕生的那一刻(138億年前)開始,每一秒都搖一次盒子,一直搖到今天,也遠遠搖不出一次盒子2的情況(機率太低了)。
